Calcolo dell'interesse composto e calcolo della rata:

Forse, non tutti sanno che esistono due modi per calcolare il saggio di interesse annuo da applicare al piano di ammortamento quando la cadenza del pagamento delle rate è inferiore all'anno. Nella prassi bancaria, viene applicata una formula, meno vantaggiosa per il debitore, che differisce da quella applicata da altri enti non economici e a mio avviso più corretta dal punto di vista finanziario. C'è comunque da dire che questo sistema di calcolo è da sempre accettato ed utilizzato in tutto il mondo. Tenterò di spiegarlo partendo dalla formula del montante. La formula del Montante (M) cioè del capitale che otterrò con un investimento iniziale (C) ad un determinato tasso di interesse composto (i) in base alla durata t è:

 

M= C (1+i)t 



Gli istituti di credito quando pubblicizzano il tasso di interesse sui prestiti fanno riferimento ad un tasso annuo, ad esempio il 3 % annuo.

Nella restituzione del capitale applicano l'interesse in base alle cadenze di pagamento.

Nel caso di rata mensile ad esempio l'interesse annuo (es. 3%) viene diviso per 12 (mesi).

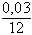Quindi il saggio di interesse del 3 % annuo diventa  3%   che è uguale a 0,0025.

 

Ora se applichiamo il saggio alla formula dell'interesse composto otteniamo per una unità di capitale  il montante:  

                    M= C (1+i)t  == >    M = (1+0,0025)12        == >   1,030415957


cioè un interesse annuo dello 0,030415957 che è più del 3% .


        Il secondo metodo per applicare il tasso del 3% annuo su base mensile utilizza il calcolo finanziario di conversione del tasso  annuo in mensile:

formula tasso 2



cioè nel caso del 3% annuo sarà uguale ad un tasso mensile di:


 

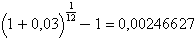
interesse



quindi se applichiamo il saggio alla formula dell'interesse composto avremo per una unità di capitale il montante di  

 

M= C (1+i)t  == >    M = (1+0,00246627) 12        == >   1,030000003

 

ottentendo un interesse annuo dello 0,030000003   che è prossimo al  3 %

Infine, passiamo ad applicare i tassi di interesse come sopra determinati per calcolare la rata di ammortamento.

Le formula da applicare per il calcolo della della rata di ammortamento (metodo francese) è :  

 


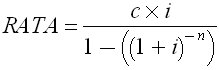
     Per eventuali confronti tra i due metodi di calcolo dell'interesse per il calcolo della rata di mutuo,  potete utilizzare le funzioni messe a disposizione nella  homepage  dove  verrà costruito il piano di ammortamento con la rata e la  rispettiva quota di interesse e capitale.
 

Nel caso del pagamento di un mutuo con cadenza mensile di pagamento la quota interessi di ciascuna rata viene calcolata così:

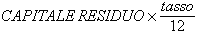  •                                      Calcolo prassi bancaria 
  •                  Calcolo  finanziario

Concludendo, aggiungo qui sotto la tabella comparativa dei due metodi di calcolo della rata con tre ipotetici tassi annuali di interesse.

100.000 euro x 20 anni 3% 6% 9%
Banche, Finanziarie 555 716 900
Calcolo finanziario 553 707 877
Differenza rata mensile 2 9 33